Let's look at a common argument made on the subject encapsulated in a conversation from the play The Trial of God by Ellie Wiesel. The play takes place on Purim 1649 in the town of Shamgorod a year after a brutal pogrom had wiped out the town's Jewish population save an innkeeper (Berish) and his daughter (Hanna). As part of an impromtu Purim shpiel the innkeeper and his guests set up a Beis Din (Jewish court) and put God himself on trial, with Berish acting as prosecuter and a stranger named Sam acting as defense attorney. Here is an excerpt from the play:
BERISH
A lie, it’s a lie! There are a thousand ways to suffer, but
only one way to die—and death is always cruel, unjust, inhuman.
SAM
No, my dear Prosecutor. In these matters I am a greater expert
than you. There are moments of death more cruel than others.
BERISH
You’re telling me? More cruel, yes! Less cruel, no! (To the court) Take Reb Hayim the scribe,
who never squashed a fly or an ant, for they too are God’s living creatures; I
sam him in agony, I want to know: Who willed his agony? Take Shmuel the
cobbler, who treated strangers as though they were his own children; I saw his
tears, his last tears. I demand an answer: Who was thirsty for his blood? I
want to know: Why was Reb Yiddel the cantor murdered? Or Reb Monish his
brother? Why were Hava the orphan and her little brother Zisha murdered? So
that they could say thank you—and I could say thank you?
SAM
Again you speak for them? You act as though they had appointed
you their spokesman. Have they? You knew them—so what? Alive, they were yours;
dead, they belong to someone else. The dead belong to the dead, and together
they form an immense community reposing in God and loving Him the way you have
never loved and never will! (To the court) He is asking, Why
murder—why death? Pertinent questions. But we have some more: Why evil—why
ugliness? If God chooses not to answer, He must have his reasons. God is God,
and His will is independent from ours—as is His reasoning.
MENDEL
What is there left for us to do?
SAM
Endure. Accept. And say Amen.
BERISH
Never! If He wants my life, let Him take it. But He has taken
other lives—Don’t tell me they were happy to submit to His will—don’t tell me
they’re happy now! If I’m not, and I’m alive, how can they be? True, they are
silent. Good for them and good for Him. If they choose to be silent, that’s
their business! I shall not be!
SAM
That is understandable. They saw His charity and grace; you did
not.
BERISH
Maria, you are right. He is
repulsive. (To SAM) How can you speak
of grace and charity after a program?
SAM
Is there a more propitious time to speak about them? You are
alive—isn’t that a proof of His kindness?
BERISH
The Jews of Shamgorod perished—isn’t that a proof of His lack
of kindness?
SAM
You are obsessed with the dead; I only think of the living.
BERISH
And what if I told you that He spared me not out of kindness
but out of cruelty?
SAM
He spared you, and you are against Him.
BERISH
He annihilated Shamgorod and you want me to be for Him? I
can’t! If He insists upon going on with His methods, let Him—but I won’t say
Amen. Let Him crush me, I won’t say Kaddish. Let Him kill me, let Him kill us
all, I shall shout and shout that it’s His fault. I’ll use my last energy to
make my protest known. Whether I live or die, I submit to Him no longer.
In this conversation, Sam is making two arguments I have heard frequently among theists when discussing this topic.
One is the defence that one cannot know the mind of God or that God's ways are mysterious to human beings, thus we have no way of knowing if any event, including gratuitous suffering, is ever truly bad in the big picture. Perhaps the suffering serves some divine purpose that we are unable to comprehend, but if we were to comprehend it we wouldn't consider it wrong. Thus suffering of any kind can never be evidence against God's existence since one can't say God wouldn't allow for it to occur. I will call this argument (A).
The other argument Sam makes is to look at all of the positive events around us. Surely the fact that Berish and his daughter survived, although traumatized, is nothing short of a miracle. Additionally, Sam says he prefers to focus on the positive, all the good things in this world that point towards God's existence. This is further emphasized in the way Sam argues in the following passage when one of the Judges, Mendel, discusses a pogrom he experienced:
MENDEL
Sabbath morning. A crowded synagogue—more crowded than usual.
I stood on the bimah before the open scrolls and read. That Shabbat we read the
commandment to celebrate our holidays in joy. I had hardly finished the
sentence when the doors were pushed open. The mob took over. The killers were
laughing. I remember their laughter as I remember their shiny swords. Minutes
later, it was all over. Not one Jew cried out; we didn’t have the time. As I heard
the echo of my own words: “And you shall celebrate your holidays in joy”—I
found myself without a community. I was still standing; I stood throughout the
slaughter. Standing before the open parchments. Why was I spared? Is it
possible that they failed to see me because I was standing? I saw blood, only
blood. I felt swept by madness. I whispered over and over again: “And you shall
celebrate your holidays in joy, in joy, in joy.” And I backed out and left.
SAM
Blessed be the Lord for His miracles.
MENDEL
A whole community was massacred, and you talk of miracles.
SAM
A Jew survived, and you ignore them?
Hence, if a truly remarkable and positive thing occurs this is surely evidence, if not proof, of God's existence. I will call this argument (B).
The problem with these arguments is that they are completely inconsistent.
To show why these arguments are incompatable we can look to Bayes' Theorem.
The problem with these arguments is that they are completely inconsistent.
To show why these arguments are incompatable we can look to Bayes' Theorem.
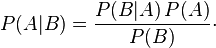
Bayes' Theorem defines the relationship between unconditional and conditional probabilities, but more than that it helps us understand the best way to adjust our beliefs based on evidence.
Probability can be understood as the degree of belief or confidence one has in a proposition. For example one could say that you have 20% confidence that it will rain today. We could represent that degree of belief or confidence in probability notation as
P(It will rain today) = 20%
Yet lets say that if you observe rain clouds outside your confidence that it will rain today goes up, that can be represented as follows:
Probability can be understood as the degree of belief or confidence one has in a proposition. For example one could say that you have 20% confidence that it will rain today. We could represent that degree of belief or confidence in probability notation as
P(It will rain today) = 20%
Yet lets say that if you observe rain clouds outside your confidence that it will rain today goes up, that can be represented as follows:
P(It will rain today|Rain clouds are in the Air) = 80%
The notation of " | " above simply means given. Thus the probability (or your confidence) it will rain today given you see rain clouds is 80%. Your degree of beliefs in propasitions change as you gain relevant evidence.
What Bayes' Rule tells us is how evidence (in the above formula "B") alters our beliefs ("A" above) and we can see that by comparing P(A), the prior belief of A before evaluating the evidence, to P(A|B), the posterior belief after evaluating evidence B.
There is a lot of contention when it comes to how the prior probabilities are set, but for our purposes here I don't really care about what actual numbers are applied to the prior. The only thing I wish to evaluate is the relationship between the prior and posterior probabilities. If P(A) > P(A|B) then that means the evidence B diminishes belief in A. If P(A) < P(A|B) then that means the evidence B increases belief in A. If P(A) =P(A|B) then that means the evidence B has no effect on the belief in A.
Applying Bayes' Rule to the arguments above we can define some notation.
- Let's say T is the "event" that "theism is true" (that a God as described above exists)
- Additionally E1 is a remarkably positive event (let's say a person surviving a pogrom as Mendel did above)
- And E2 is a remarkably negative event (say a child is murdered in a particularly heinous way)
Using these terms we can set up Bayes' Rule as follows:
P(T|E) = P(E|T) x P(T)
P(E|T) x P(T) + P(E|not-T) x P(not-T)
Translating the arguments A & B into probability notation we get:
(A) Suffering (or any event E2) can never be evidence against Gods existence can be written as follows: P(T) < or = P(T|E2), otherwise if P(T) > P(T|E2) then this means that this evidence E2 diminishes the belief that T or God exists.
But following Bayes' rule, regardless of how the other variables end up, unless the theist wishes to argue that not seeing a remarkably negative event is evidence against God, they are forced to say that P(T) = P(T|E2) = P(T|not-E2). Or in other words evidence of this type has no effect on ones belief in God.
(B) Amazing events (or any event E1) is positive evidence for God can be written as P(T) < P(T|E1).
Now here is the problem, for any evidence (say E1 in this case) that steers ones belief in any one direction, in the situation where the evidence is not observed to occur (not-E1) necessarily results in P(T) > P(T|not-E1). Thus using the example above, Mendel not surviving the Pogrom would result in a diminishing of belief.
But how could that be so in light of argument (A)? How could a non remarkable negative event such as this (it is hardly surprising for a person to die in a pogrom under those conditions) result in a diminishing of belief in God, whereas a surprising negative event such as E2 not effect any change whatsoever?
The reason is because E1 & E2 are essentially the same type of evidence (we could categorize them under the label E) and we can see that the the arguments (A) P(T) = P(T|E) and (B) P(T) < P(T|E) are mathematically contradictory. It is inconsistent to argue that negative events cannot imply anything about God since God's ways are mysterious and then to turn around, as Sam does in the play, and argue that positive events imply that God does exist as God's ways are Just, Moral & Good. You can't have your cake and eat it too.
Now there is nothing to stop a theist from adopting either argument, but they must only choose one. If they choose (A) they can combat evidence of the form E2, but have no way of using positive events (even to the extent of not being able to argue for Divine Providence I suppose) of the form E1 as evidence for God. If they choose (B) they can use remarkable things to indicate God's existence, but for every remarkable thing, their belief in God must be diminished by the negative events E2 (which IMO far outweigh events of type E1).
Which approach do you consider more reasonable?
Which approach do you consider more reasonable?